
Informatyka 2
Treści usunięte z lekcji zgodnie z podstawą programową
z 2024 r. sprawdź w e-booku podręcznika na eduranga.pl.
z 2024 r. sprawdź w e-booku podręcznika na eduranga.pl.
FilmProgramowanie w Pythonie. Algorytmy zachłanne. Wiele monet
Film omawia stosowanie algorytmów zachłannych na przykładzie wydawania reszty przy użyciu minimalnej liczby monet.
InfografikaSortowanie okiem informatyka
Infografika omawia różne sposoby porządkowania zbioru danych względem pewnych cech charakterystycznych każdego elementu tego zbioru.
Film 1Sortowanie bąbelkowe, przez wstawianie i przez prosty wybór
W filmie umówiono trzy podstawowe algorytmy sortowania (bąbelkowe, przez wstawianie i przez prosty wybór) oraz przedstawiono ich działanie na przykładach.
karty © Francesco Abrignani/Shutterstock.com
Film 2Programowanie w Pythonie. Porządkowanie przez proste wybieranie
Film powtórzeniowy, prezentujący sortowanie przez proste wybieranie realizowane w Pythonie.
Ćwiczenie 0
Zdefiniuj funkcję trzy(a, b, c), której wynikiem jest największa z trzech liczb podanych jako parametr. Sprawdź działanie funkcji dla podanych poniżej parametrów.
- Wynikiem funkcji
trzy(1, 9, 12)jest12. - Wynikiem funkcji
trzy(13, 4, 12)jest13.
Wskazówka
Na początku za największą liczbę przyjmuje się pierwszą z trzech liczb podanych jako parametr. Następnie bada się, czy druga z liczb jest większa od niej, jeśli tak, to za największą przyjmuje się drugą liczbę. Następnie bada się, czy trzecia z liczb jest większa od niej, jeśli tak, to za największą przyjmuje się trzecią liczbę.
Film 1Programowanie w Pythonie. Badanie własności liczb całkowitych. Liczby pierwsze
W filmie omówiono algorytm sprawdzający, czy dana liczba jest pierwsza, oraz pokazano jego implementację.
Film 2Programowanie w Pythonie. Suma dzielników liczby
Film prezentuje zagadnienie złożoności czasowej algorytmu na przykładzie badania własności liczb całkowitych, a konkretnie badania sumy dzielników danej liczby.
Ćwiczenie 0
Zdefiniuj funkcję czy_parzysta(n), której wynikiem jest True w przypadku, gdy liczba podana jako parametr jest parzysta, lub False, gdy jest nieparzysta. Sprawdź działanie funkcji dla podanych poniżej parametrów.
- Wynikiem funkcji
czy_parzysta(1)jestFalse. - Wynikiem funkcji
czy_parzysta(2)jestTrue.
Wskazówka
Zauważ, że algorytm sprawdzania parzystości liczby opiera się na badaniu reszty z dzielenia liczby przez 2. Jeśli ta reszta równa jest 0, to liczba jest parzysta, w przeciwnym wypadku – nieparzysta.
FilmyProgramowanie w Pythonie – filmy powtórzeniowe
Prezentacja 1Sposoby przedstawiania algorytmów
Prezentacja omawia zapis algorytmu za pomocą języka naturalnego, w postaci listy kroków (pseudokodu), schematu blokowego i programu.
Prezentacja 2Python – powtórzenie
Prezentacja przedstawia najważniejsze konstrukcje stosowane w języku Python.
PlanszaPython – podstawowe polecenia
Plansza zawiera podstawowe operatory działań i porównania oraz polecenia.
InfografikaPowtarzanie tych samych operacji, czyli pętle
Infografika pokazuje, czym pętla while różni się od pętli for.
Ćwiczenie 0
Przećwicz posługiwanie się pętlą while. Zdefiniuj funkcję ile_cyfr(liczba), której wynikiem będzie liczba cyfr danej liczby. Sprawdź działanie funkcji dla podanych poniżej parametrów.
- Wynikiem funkcji
ile_cyfr(123)jest3. - Wynikiem funkcji
ile_cyfr(17923)jest5.
Ćwiczenie 0
Zaopatrzeniowiec dostaje listę zakupów. Martwi się, aby nie przekroczyć dopuszczalnego udźwigu po załadowaniu samochodu. Zdefiniuj funkcję zakupy(c, m, z), której parametrami są liczby worków c – cukru, m – mąki i z – ziemniaków. Worki cukru ważą 2 kg, mąki 5 kg i ziemniaków 12 kg. Udźwig samochodu wynosi 500 kg. Wynikiem funkcji jest True, gdy samochód może przewieźć zakupy, lub False, gdy zostanie przekroczony udźwig. Sprawdź działanie funkcji dla podanych poniżej parametrów.
- Wynikiem funkcji
zakupy(4, 9, 12)jestTrue. - Wynikiem funkcji
zakupy(12, 34, 43)jestFalse.
Wskazówka
Należy znaleźć łączną wagę produktów, a potem porównać wynik z 500. Łączną wagę produktów obliczamy, mnożąc liczbę worków przez ich masy, potem poszczególne liczby dodajemy do siebie.
Ćwiczenie 1Czy liczba jest pierwsza?
Zdefiniuj funkcję logiczną czy_pierwsza(n), której parametrem jest liczba naturalna n większa od 1, a wynikiem wartość True, gdy jest ona liczbą pierwszą, albo False, gdy nią nie jest. Sprawdź działanie funkcji dla podanych poniżej parametrów.
- Wynikiem funkcji
czy_pierwsza(11)jestTrue. - Wynikiem funkcji
czy_pierwsza(99)jestFalse.
Ćwiczenie 1Podział na rzędy
W międzynarodowej konferencji weźmie udział określona liczba gości z różnych krajów i określona liczba gospodarzy. Zaproszeni będą siedzieć w rzędach tak, aby każdy rząd był równoliczny i w każdym siedzieli albo tylko goście, albo tylko gospodarze. Jaka jest największa możliwa liczba osób w każdym rzędzie? Zdefiniuj funkcję rzad(goscie, gospodarze), której parametrami są liczba gości i gospodarzy, a wynikiem jest liczebność rzędu. Sprawdź działanie funkcji dla podanych poniżej parametrów.
- Wynikiem funkcji
rzad(72, 90)jest18. - Wynikiem funkcji
rzad(24, 36)jest12.
Ćwiczenie 2Podział na grupy
Na potrzeby warsztatów należy podzielić gości i gospodarzy na możliwie małe zespoły tak, by w każdym zespole była jednakowa liczba osób (gości i gospodarzy). Zdefiniuj funkcję ile(goscie, gospodarze), której parametrami są liczba gości oraz liczba gospodarzy, a wynikiem jest liczebność każdego zespołu. Sprawdź działanie funkcji dla podanych poniżej parametrów.
- Wynikiem funkcji
ile(56, 42)jest7. - Wynikiem funkcji
ile(25, 35)jest12.
Ćwiczenie 3Spotkania zespołów
Organizacją konferencji zajmują się dwa zespoły: do spraw programowych i do spraw metodycznych. Pierwszy spotyka się co x dni, drugi co y. Dziś spotkały się oba zespoły. Zdefiniuj funkcję kiedy(x, y), w której jako parametry będziesz podawać, co ile dni spotykają się zespoły, a wynikiem będzie liczba dni, które upłyną do następnego wspólnego spotkania obu zespołów. Sprawdź działanie funkcji dla podanych poniżej parametrów.
- Wynikiem funkcji
kiedy(6, 4)jest12. - Wynikiem funkcji
kiedy(9, 12)jest36.
Ćwiczenie 4Sprytne zakupy
Każdy gość powinien dostać taką samą liczbę długopisów, ołówków i flamastrów. Zdefiniuj funkcję flamastry(x, y, z), której parametrami są liczba długopisów w paczce (x), liczba ołówków w paczce (y) i liczba sztuk flamastrów w paczce (z), a wynikiem jest najmniejsza liczba opakowań flamastrów, które gospodarze powinni kupić, aby nic nie zostało. Sprawdź działanie funkcji dla podanych poniżej parametrów.
- Wynikiem funkcji
flamastry(6, 8, 10)jest12. - Wynikiem funkcji
flamastry(39, 26, 52)jest3.
Ćwiczenie dodatkowe 1
Przećwicz posługiwanie się pętlą while. Zdefiniuj funkcję suma_cyfr(liczba), której wynikiem jest suma cyfr liczby. Sprawdź działanie funkcji dla podanych poniżej parametrów.
- Wynikiem funkcji
suma_cyfr(123)jest6. - Wynikiem funkcji
suma_cyfr(17923)jest22.
Wskazówka
Zauważ, że algorytm sumowania cyfr opiera się na wyodrębnianiu cyfr od końca i kolejno ich sumowania. W każdym kroku wyliczana jest ostatnia cyfra jako reszta dzielenia przez 10 oraz liczba jest dzielona przez 10.
Ćwiczenie dodatkowe 2
Przećwicz posługiwanie się pętlą while. Zdefiniuj funkcję iledo6(lista), której wynikiem jest liczba liczb, które na liście są wpisane przed liczbą 6. Przyjmij, że 6 występuje co najmniej raz. Sprawdź działanie funkcji dla podanych poniżej parametrów.
- Wynikiem funkcji
iledo6([1, 2, 3, 4, 5, 6, 7])jest5. - Wynikiem funkcji
iledo6([1, 6, 3, 5, 5, 6, 7])jest1.
Ćwiczenie dodatkowe 3
Przećwicz posługiwanie się pętlą while. Zdefiniuj funkcję suma(lista), której wynikiem jest suma liczb, które na liście są wpisane przed liczbą 0. Przyjmij, że 0 występuje co najmniej raz. Sprawdź działanie funkcji dla podanych poniżej parametrów.
- Wynikiem funkcji
suma([1, 2, 3, 4, 0, 6, 7])jest10. - Wynikiem funkcji
suma([1, 2, 0, 4, 5, 6, 0])jest3.
Ćwiczenie dodatkowe 4
Przećwicz posługiwanie się pętlą while. Zdefiniuj funkcję sumap(lista), której wynikiem jest suma liczb parzystych, które na liście są wypisane przed liczbą 0. Przyjmij, że 0 występuje co najmniej raz. Sprawdź działanie funkcji dla podanych poniżej parametrów.
- Wynikiem funkcji
sumap([1, 2, 3, 4, 0, 6, 7])jest6. - Wynikiem funkcji
sumap([2, 2, 2, 4, 2, 6, 0])jest18
Ćwiczenie dodatkowe 5
Przećwicz posługiwanie się pętlą while. Zdefiniuj funkcję sumanp(lista), której wynikiem jest suma liczb nieparzystych, które na liście są wypisane przed liczbą 0. Przyjmij, że 0 występuje co najmniej raz. Sprawdź działanie funkcji dla podanych poniżej parametrów.
- Wynikiem funkcji
sumanp([1, 2, 3, 4, 0, 6, 7])jest4. - Wynikiem funkcji
sumanp([2, 2, 2, 4, 2, 6, 0])jest0.
Pytania quizoweAlgorytm Euklidesa w praktyce
-
Czy w algorytmie Euklidesa z odejmowaniem można zastąpić krok „Wynikiem jest
a” krokiem „Wynikiem jestb”? -
-
Czy przy dodawaniu dwóch ułamków zwykłych krok „Znajdź wspólny mianownik
m = NWW(b, d)” można zastąpić krokiem „Znajdź wspólny mianownikm = b * d”? -
-
Jeśli warunek pętli
whilezapisano jakox <= 10, przy czym w pętli tej nie jest modyfikowana wartośćx, to ile razy wykona się pętla dla wartości początkowejx = 3? -
Ćwiczenie 2N-ta liczba pierwsza
Zdefiniuj funkcję pierwsza(n), której parametrem będzie liczba naturalna n, a wynikiem – n-ta liczba pierwsza. Sprawdź działanie funkcji dla podanych poniżej parametrów.
- Wynikiem funkcji
pierwsza(7)jest17. - Wynikiem funkcji
pierwsza(25)jest97.
Ćwiczenie 3Liczby bliźniacze
Liczby bliźniacze to liczby pierwsze różniące się o 2. W pierwszej setce jest osiem par takich liczb: 3 i 5, 5 i 7, 11 i 13, 17 i 19, 29 i 31, 41 i 43, 59 i 61, 71 i 73. Zdefiniuj funkcję blizniacze(n), której parametrem jest liczba naturalna n, a wynikiem pierwsza liczba z n-tej pary liczb bliźniaczych. Sprawdź działanie funkcji dla podanych poniżej parametrów.
- Wynikiem funkcji
blizniacze(3)jest11. - Wynikiem funkcji
blizniacze(7)jest59.
Ćwiczenie 4Suma dzielników liczby
Zdefiniuj funkcję suma_dzielnikow(n), której parametrem jest liczba naturalna n, a wynikiem – suma dzielników tej liczby. Sformułuj dwa algorytmy i porównaj szybkość działania każdego z nich dla różnych danych. Sprawdź działanie funkcji dla podanych poniżej parametrów.
- Wynikiem funkcji
suma_dzielnikow(7)jest8. - Wynikiem funkcji
suma_dzielnikow(16)jest31.
Algorytm sprawdzający podzielność danej liczby przez kolejne liczby naturalne – od 1 do niej samej.
Algorytm sprawdzający podzielność danej liczby przez kolejne dzielniki od 2 do pierwiastka z tej liczby.
Ćwiczenie 5Liczby zaprzyjaźnione
Liczby zaprzyjaźnione to dwie liczby naturalne, z których każda jest równa sumie dzielników właściwych drugiej liczby (np. suma dzielników właściwych liczby 220 wynosi 284, a suma dzielników właściwych liczby 284 – 220). Zdefiniuj funkcję zaprzyjaznione(n), której parametrem jest liczba naturalna n, a wynikiem – mniejsza liczba z n-tej pary liczb zaprzyjaźnionych. Sprawdź działanie funkcji dla podanych poniżej parametrów.
- Wynikiem funkcji
zaprzyjaznione(1)jest220. - Wynikiem funkcji
zaprzyjaznione(3)jest2620.
Ćwiczenie dodatkowe 1
Zdefiniuj funkcję parzyste(liczba1, liczba2), której parametrami są liczby całkowite dodatnie, przy czym liczba1 < liczba2, a ich różnica wynosi co najmniej 3. Wynikiem funkcji jest lista dwóch liczb – najmniejszej liczby parzystej większej od parametru liczba1 i największej liczby parzystej mniejszej od parametru liczba2. Sprawdź działanie funkcji dla podanych poniżej parametrów.
- Wynikiem funkcji
parzyste(4, 9)jest[6, 8]. - Wynikiem funkcji
parzyste(9, 12)jest[10, 10]. - Wynikiem funkcji
parzyste(14, 75)jest[16, 74].
Ćwiczenie dodatkowe 2
Zdefiniuj funkcję nieparzyste(n), której wynikiem jest liczba liczb nieparzystych podzielnych przez 7 nie większych od parametru n. Sprawdź działanie funkcji dla podanych poniżej parametrów.
- Wynikiem funkcji
nieparzyste(30)jest2. - Wynikiem funkcji
nieparzyste(35)jest3. - Wynikiem funkcji
nieparzyste(100)jest7.
Ćwiczenie dodatkowe 3
Liczby lustrzane to takie dwie liczby, które są lustrzanym odbiciem, np.: 123 i 321, 79 i 97, 1245 i 5421. Jeżeli zapiszemy razem dowolną liczbę i jej lustrzane odbicie, np. 123321, to tak otrzymana liczba jest podzielna przez 11.
Na przykład:
123321 : 11 = 11211
7997 : 11 = 727
12455421 : 11 = 1132311
Zdefiniuj funkcję lustro_11(liczba), której parametrem jest liczba całkowita dodatnia, a wynikiem iloraz liczby i doklejonej do niej jej liczby lustrzanej przez 11. Sprawdź działanie funkcji dla podanych poniżej parametrów.
- Wynikiem funkcji
lustro_11(123)jest11211(ponieważ 123321 : 11 = 11211). - Wynikiem funkcji
lustro_11(893)jest81218(ponieważ 893398 : 11 = 81218).
Ćwiczenie dodatkowe 4
Zdefiniuj funkcję dwie(liczba), której wynikiem jest suma cyfr jedności i dziesiątek danej liczby powiększona o 1, gdy suma okazała się liczbą nieparzystą, lub zmniejszona o 1, gdy suma okazała się liczbą parzystą. Parametr liczba przyjmuje wartości z zakresu od 10 do 1 000 000. Sprawdź działanie funkcji dla podanych poniżej parametrów.
- Wynikiem funkcji
dwie(1284456)jest12. - Wynikiem funkcji
dwie(892339)jest11.
Zadanie 1Liczby czworacze
Liczby czworacze to liczby pierwsze mające postać: n, n + 2, n + 6 i n + 8. Zdefiniuj funkcję czworacze(n), której parametrem jest liczba naturalna n, a wynikiem – lista takich liczb czworaczych, w których pierwsza liczba jest większa od podanego parametru. Sprawdź działanie funkcji dla podanych poniżej parametrów.
- Wynikiem funkcji
czworacze(9)jest[11, 13, 17, 19]. - Wynikiem funkcji
czworacze(150)jest[191, 193, 197, 199].
Zadanie 2Problem Collatza
Pierwsza liczba ciągu Collatza jest dowolną liczbą naturalną x, a każda kolejna wartość ciągu obliczana jest na podstawie poprzedniej według poniższych zasad:
- jeśli poprzednia wartość była parzysta, to należy podzielić ją przez 2;
- jeśli poprzednia wartość była nieparzysta, to należy pomnożyć ją przez 3 i dodać 1.
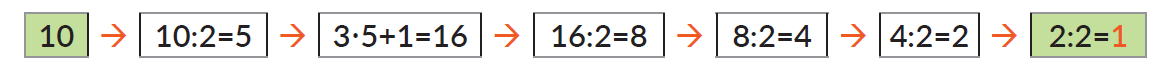
Przypuszcza się, że niezależnie od której liczby naturalnej zaczniemy, zawsze po pewnej skończonej liczbie kroków otrzymamy liczbę 1. (Udowodniono to dla liczb mniejszych niż kilka tryliardów).
Zdefiniuj funkcję collatz(x), której parametrem jest liczba naturalna x, czyli wartość początkowa ciągu liczb Collatza, a wynikiem – liczba kroków, po których w ciągu pojawi się liczba 1. Sprawdź działanie funkcji dla podanych poniżej parametrów.
- Wynikiem funkcji
collatz(10)jest6. - Wynikiem funkcji
collatz(15)jest17.
Zadanie 3Suma kwadratów cyfr
Polski matematyk Hugo Steinhaus zauważył, że jeśli zsumujemy kwadraty cyfr wybranej liczby naturalnej, a następnie będziemy sumować kwadraty cyfr kolejnych otrzymanych liczb, to w pewnym momencie zawsze otrzymamy 1 lub 4. Zdefiniuj funkcję suma_kwadratow(n), której wynikiem będzie suma kwadratów cyfr liczby podanej jako parametr. Przetestuj działanie dla liczby 123 i kilku innych liczb początkowych.
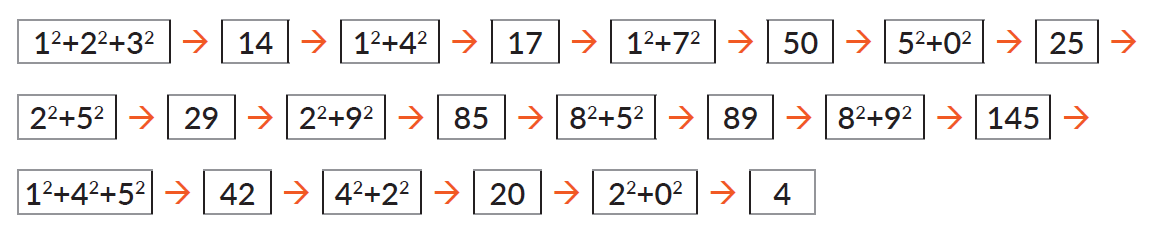
Pytania quizoweBadanie własności liczb całkowitych
-
Jak nazywa się algorytm znajdowania liczb pierwszych w podanym zakresie?
-
-
W jakim przedziale algorytm optymalny będzie szukał dzielników liczby 10 000?
-
-
Co określa czasowa złożoność obliczeniowa?
-
Ćwiczenie 1Tworzenie listy i dodawanie do niej elementów
Przeanalizuj poniższy kod, odpowiedz na pytania, a następnie sprawdź swoje odpowiedzi
w edytorze.
- Jaki element i gdzie dodano do listy za pomocą polecenia w wierszu 2?
- Jak należy uzupełnić wiersz 3, aby na końcu listy wstawić liczbę –11?
- Jak poprawić zapis w wierszu 4, aby liczba 0 została wstawiona na początku listy, a liczba 23 na jej końcu?
- Jaki element i na której pozycji dodano do listy za pomocą polecenia w wierszu 5?
- Jaka lista zostanie wypisana na skutek polecenia w wierszu 6?
Ćwiczenie 2Losowa lista liczb
Zdefiniuj funkcję losuj(rozmiar, od, do) służącą do generowania listy o podanej długości (rozmiar), której elementami są liczby losowe z podanego zakresu (od i do).
Ćwiczenie 3Bąbelek
Porównaj kolejne pary elementów listy (pierwszy z drugim, drugi z trzecim itd.). Jeśli pierwszy z nich jest większy niż drugi, to zamień je miejscami. Przeanalizuj dane (zauważ, że największa z liczb w wyniku znalazła się na końcu) i zdefiniowaną poniżej funkcję b(t), której parametrem jest lista liczb, a wynikiem – zmodyfikowana lista. Następnie znajdź i popraw błąd w skrypcie.
- Wynikiem funkcji
b([16, 5, 12, 3, 12])jest[5, 12, 3, 12, 16]. - Wynikiem funkcji
b([1, 16, 18, 3, 16, 9, 9])jest[1, 16, 3, 16, 9, 9, 18].
Ćwiczenie 4Sortowanie bąbelkowe
Zdefiniuj funkcję sort_b(t), której wynikiem jest podana jako parametr lista t, posortowana metodą bąbelkową w porządku rosnącym. Sprawdź działanie funkcji dla podanych poniżej parametrów.
- Wynikiem funkcji
sort_b([6, 3, 15, 9, 2])jest[2, 3, 6, 9, 15]. - Wynikiem funkcji
sort_b([11, 16, 8, 33, 6, 8, 1])jest[1, 6, 8, 8, 11, 16, 33].
Ćwiczenie 5Wstawianie elementów
Zdefiniuj funkcję w(t, x), której parametrami są posortowana lista liczb t oraz liczba x, a wynikiem jest lista t
z liczbą x wstawioną w odpowiednim miejscu. Sprawdź działanie funkcji dla podanych poniżej parametrów.
- Wynikiem funkcji
w([6, 13, 15, 19, 22], 18)jest[6, 13, 15, 18, 19, 22]. - Wynikiem funkcji
w([1, 9, 12, 33, 46], 57)jest[1, 9, 12, 33, 46, 57]. - Wynikiem funkcji
w([-4, -2, 0, 2, 4], 0)jest[-4, -2, 0, 0, 2, 4].
Ćwiczenie 6Sortowanie przez wstawianie
Uzupełnij definicję funkcji sort_w(t), której wynikiem jest podana jako parametr lista t, posortowana metodą przez wstawianie w porządku rosnącym. Sprawdź działanie funkcji dla podanych poniżej parametrów.
- Wynikiem funkcji
sort_w([6, 3, 15, 9, 2])jest[2, 3, 6, 9, 15]. - Wynikiem funkcji
sort_w([11, 16, 8, 33, 6, 8, 1])jest[1, 6, 8, 8, 11, 16, 33].
Ćwiczenie dodatkowe 1
Zdefiniuj funkcję minimum(liczba), której wynikiem będzie najmniejsza cyfra liczby podanej jako parametr. Parametrem jest co najmniej dwucyfrowa liczba całkowita dodatnia. Sprawdź działanie funkcji dla podanych poniżej parametrów.
- Wynikiem
minimum(19)jest1. - Wynikiem
minimum(98989)jest8.
Ćwiczenie dodatkowe 2
Zdefiniuj funkcję ile_liczb(tab), której wynikiem jest liczba różnych liczb na liście podanej jako parametr. Parametrem jest niepusta lista co najwyżej 100 liczb z zakresu od 0 do 10. Sprawdź działanie funkcji dla podanych poniżej parametrów.
- Wynikiem funkcji
ile_liczb([4, 1, 1, 4])jest2. - Wynikiem funkcji
ile_liczb([6, 6, 3, 7, 1, 7, 4, 4, 0, 3])jest6.
Pytania quizoweSortowanie bąbelkowe i przez wstawianie
-
W programie zadeklarowano listę
tab = [-3, 4, -12, 0, 3]. Jaką wartość będzie miała zmiennatabpo operacjitab = tab + [2]? -
-
W programie zadeklarowano listę
tab = [-3, 4, -12, 0, 3]. Jaką wartość ma element o indeksie3? -
-
W programie wykonano poniższe operacje.
x = 5
y = 3
x = y
y = x
Ile wynoszą wartości zmiennychxiy? -
Ćwiczenie 1Trzy monety
Dysponujesz nieograniczoną liczbą monet o nominałach 5, 3 i 1 i masz wydać resztę przy użyciu minimalnej liczby monet. Zdefiniuj funkcję trzy(kwota), której wynikiem będzie minimalna liczba monet potrzebnych do wydania kwoty podanej jako parametr. Sprawdź działanie funkcji dla podanych poniżej parametrów.
- Wynikiem funkcji
trzy(11)jest3. - Wynikiem funkcji
trzy(99)jest21.
Ćwiczenie 2Wiele monet
Dysponujesz nieograniczoną liczbą monet o nominałach 20, 10, 5, 2 i 1 i masz wydać resztę przy użyciu minimalnej ich liczby. Zdefiniuj funkcję wiele(kwota), której wynikiem będzie minimalna liczba monet potrzebnych do wydania kwoty podanej jako parametr. Sprawdź działanie funkcji dla podanych poniżej parametrów.
- Wynikiem funkcji
wiele(11)jest2. - Wynikiem funkcji
wiele(99)jest8.
Ćwiczenie 3Ograniczona liczba monet
Dysponujesz podaną liczbą monet o określonych nominałach i masz wydać resztę przy użyciu minimalnej ich liczby. Zdefiniuj funkcję monety(kwota, nominaly, sztuki), której wynikiem będzie minimalna liczba monet potrzebnych do wydania kwoty podanej jako parametr. Sprawdź działanie funkcji dla podanych poniżej parametrów.
- Wynikiem funkcji
monety(11, [20, 10, 5, 2, 1], [100, 100, 100, 100, 100])jest2. - Wynikiem funkcji
monety(99, [20, 10, 5, 1], [1, 10, 1, 10])jest13.
Ćwiczenie dodatkowe 1
Zaopatrzeniowiec ma kupić cukier, mąkę i ziemniaki. Chce załadować jak najwięcej do samochodu, ale tak, by nie przekroczyć jego udźwigu wynoszącego x kg i przewieźć jak najmniejszą liczbę opakowań. Zdefiniuj funkcję zakupy(x), której parametrem jest udźwig, a wynikiem – łączna liczba opakowań towarów. Worki cukru ważą
2 kg, mąki 5 kg i ziemniaków 12 kg. Sprawdź działanie funkcji dla podanych poniżej parametrów.
- Wynikiem funkcji
zakupy(127)jest12. - Wynikiem funkcji
zakupy(100)jest10.
Ćwiczenie dodatkowe 2
Zaopatrzeniowiec ma kupić cukier, mąkę i ziemniaki. Chce załadować jak najwięcej do samochodu, ale tak, by nie przekroczyć jego udźwigu wynoszącego x kg i przewieźć jak najmniejszą liczbę opakowań. Dodatkowo nie może kupić więcej niż ile opakowań jednego towaru. Zdefiniuj funkcję zakupy(x, ile), której parametrami są udźwig i maksymalna liczba opakowań jednego towaru, a wynikiem jest łączna liczba opakowań towarów. Worki cukru ważą 2 kg, mąki 5 kg i ziemniaków 12 kg. Sprawdź działanie funkcji dla podanych poniżej parametrów.
- Wynikiem funkcji
zakupy(127, 9)jest14. - Wynikiem funkcji
zakupy(127, 12)jest12.
Pytania quizoweMetoda zachłanna i dynamiczna
-
Czy dla każdego typu problemów algorytmy zachłanne dają optymalne rozwiązanie?
-
-
Które ze stwierdzeń dotyczy metody zachłannej?
-
-
Na czym polega dynamiczne podejście do rozwiązania?
-
QuizAlgorytmika i programowanie w Pythonie
-
Sito Eratostenesa to algorytm znajdowania liczb pierwszych z przedziału od 2 do n. Na początek wykreślamy wszystkie wielokrotności liczby 2 większe od niej samej. Powtarzamy wykreślanie wielokrotności kolejnej niewykreślonej liczby, czyli 3, 5 itd. Jak długo musimy kontynuować wykreślanie, aby zostały wszystkie liczby pierwsze z przedziału od 2 do n?
Aż liczba, której wielokrotność wykreślamy, będzie większa niż
-
-
Wskaż zdania prawdziwe na temat pętli
foriwhile. -
-
Dokończ zdanie tak, aby było prawdziwe.
Podczas testowania algorytmów sortowania można wykorzystać
-
-
Jaki będzie wynik funkcji dla parametru 1234567987?

-
-
Jako rozwiązanie zadania uczniowie napisali poniższą funkcję:
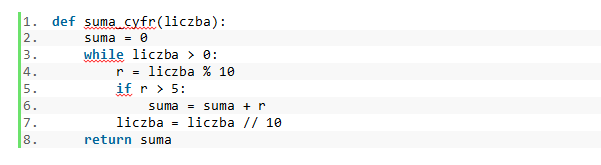
Co jest wynikiem działania funkcji dla danej liczby naturalnej?
-
-
Funkcja, która sprawdza, czy liczba podana jako parametr jest liczbą pierwszą, nie daje prawidłowych wyników. W czym tkwi problem?
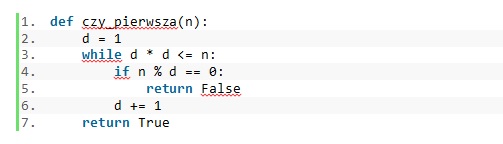
-