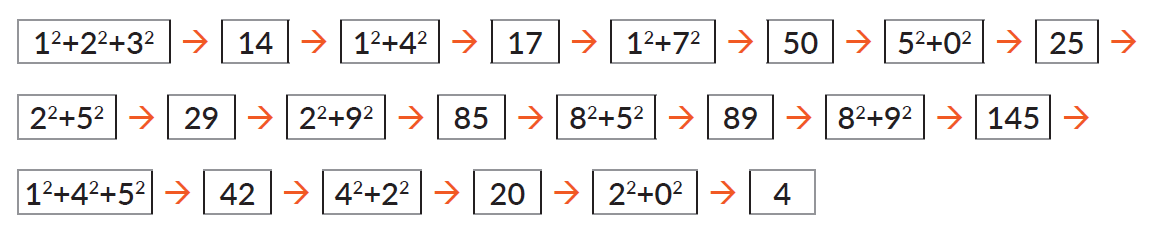W filmie omówiono algorytm sprawdzający, czy dana liczba jest pierwsza, oraz pokazano jego implementację.
Film prezentuje zagadnienie złożoności czasowej algorytmu na przykładzie badania własności liczb całkowitych, a konkretnie badania sumy dzielników danej liczby.
Zdefiniuj funkcję czy_parzysta(int n), której wynikiem jest 1 w przypadku, gdy liczba podana jako parametr jest parzysta, lub 0, gdy jest nieparzysta. Sprawdź działanie funkcji dla podanych poniżej parametrów.
czy_parzysta(1) jest 0.czy_parzysta(2) jest 1.Wskazówka
Zauważ, że algorytm sprawdzania parzystości liczby opiera się na badaniu reszty z dzielenia liczby przez 2. Jeśli ta reszta równa jest 0, to liczba jest parzysta, w przeciwnym wypadku – nieparzysta.
Zdefiniuj funkcję logiczną czy_pierwsza(int n), której parametrem jest liczba naturalna n większa od 1,
a wynikiem wartość 1, gdy jest ona liczbą pierwszą, albo 0, gdy nią nie jest. Sprawdź działanie funkcji dla podanych poniżej parametrów.
czy_pierwsza(11) jest 1.czy_pierwsza(99) jest 0.Zdefiniuj funkcję pierwsza(int n), której parametrem będzie liczba naturalna n, a wynikiem – n-ta liczba pierwsza. Sprawdź działanie funkcji dla podanych poniżej parametrów.
pierwsza(7) jest 17.pierwsza(25) jest 97.Liczby bliźniacze to liczby pierwsze różniące się o 2. W pierwszej setce jest osiem par takich liczb: 3 i 5, 5 i 7, 11 i 13, 17 i 19, 29 i 31, 41 i 43, 59 i 61, 71 i 73. Zdefiniuj funkcję blizniacze(int n), której parametrem jest liczba naturalna n, a wynikiem pierwsza liczba z n-tej pary liczb bliźniaczych. Sprawdź działanie funkcji dla podanych poniżej parametrów.
blizniacze(3) jest 11.blizniacze(7) jest 59.Zdefiniuj funkcję suma_dzielnikow(int n), której parametrem jest liczba naturalna n, a wynikiem – suma dzielników tej liczby. Sformułuj dwa algorytmy i porównaj szybkość działania każdego z nich dla różnych danych. Sprawdź działanie funkcji dla podanych poniżej parametrów.
suma_dzielnikow(7) jest 8.suma_dzielnikow(16) jest 31.Algorytm sprawdzający podzielność danej liczby przez kolejne liczby naturalne – od 1 do niej samej.
Algorytm sprawdzający podzielność danej liczby przez kolejne dzielniki od 2 do pierwiastka z tej liczby.
Liczby zaprzyjaźnione to dwie liczby naturalne, z których każda jest równa sumie dzielników właściwych drugiej liczby (np. suma dzielników właściwych liczby 220 wynosi 284, a suma dzielników właściwych liczby 284 – 220). Zdefiniuj funkcję zaprzyjaznione(int n), której parametrem jest liczba naturalna n, a wynikiem – mniejsza liczba z n-tej pary liczb zaprzyjaźnionych. Sprawdź działanie funkcji dla podanych poniżej parametrów.
zaprzyjaznione(1) jest 220.zaprzyjaznione(3) jest 2620.Zdefiniuj funkcję parzyste(int liczba1, int liczba2), której parametrami są liczby całkowite dodatnie, przy czym liczba1 < liczba2, a ich różnica wynosi co najmniej 3. Wynikiem funkcji jest suma dwóch liczb – najmniejszej liczby parzystej większej od parametru liczba1 i największej liczby parzystej mniejszej od parametru liczba2. Sprawdź działanie funkcji dla podanych poniżej parametrów.
parzyste(4, 9) jest 14.parzyste(9, 12) jest 20.parzyste(14, 75) jest 90.Zdefiniuj funkcję nieparzyste(int n), której wynikiem jest liczba liczb nieparzystych podzielnych przez 7 nie większych od parametru n. Sprawdź działanie funkcji dla podanych poniżej parametrów.
nieparzyste(30) jest 2.nieparzyste(35) jest 3.nieparzyste(100) jest 7.Zdefiniuj funkcję dwie(int liczba), której wynikiem jest suma cyfr jedności i dziesiątek danej liczby powiększona o 1, gdy suma okazała się liczbą nieparzystą, lub zmniejszona o 1, gdy suma okazała się liczbą parzystą. Parametr liczba przyjmuje wartości z zakresu od 10 do 1 000 000. Sprawdź działanie funkcji dla podanych poniżej parametrów.
dwie(1284456) jest 12.dwie(892339) jest 11.Zdefiniuj funkcję ciekawa(int n), której parametrem jest liczba naturalna n, a wynikiem – większa od podanego parametru pierwsza liczba nieparzysta, która ma nieparzystą liczbę dzielników. Sprawdź działanie funkcji dla podanych poniżej parametrów.
ciekawa(4) jest 9.ciekawa(19) jest 25.Liczby czworacze to liczby pierwsze mające postać: n, n + 2, n + 6 i n + 8. Zdefiniuj funkcję czworacze(int n), której parametrem jest liczba naturalna n, a wynikiem – pierwsza liczba z liczb czworaczych, która jest większa od podanego parametru. Sprawdź działanie funkcji dla podanych poniżej parametrów.
czworacze(9) jest 11.czworacze(150) jest 191.Pierwsza liczba ciągu Collatza jest dowolną liczbą naturalną x, a każda kolejna wartość ciągu obliczana jest na podstawie poprzedniej według poniższych zasad:
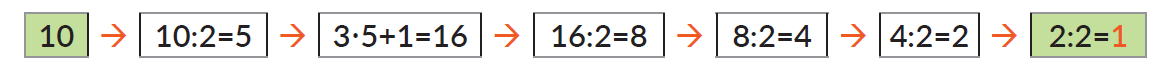
Przypuszcza się, że niezależnie od której liczby naturalnej zaczniemy, zawsze po pewnej skończonej liczbie kroków otrzymamy liczbę 1. (Udowodniono to dla liczb mniejszych niż kilka tryliardów).
Zdefiniuj funkcję collatz(int x), której parametrem jest liczba naturalna x, czyli wartość początkowa ciągu liczb Collatza, a wynikiem – liczba kroków, po których w ciągu pojawi się liczba 1. Sprawdź działanie funkcji dla podanych poniżej parametrów.
collatz(10) jest 6.collatz(15) jest 17.Polski matematyk Hugo Steinhaus zauważył, że jeśli zsumujemy kwadraty cyfr wybranej liczby naturalnej, a następnie będziemy sumować kwadraty cyfr kolejnych otrzymanych liczb, to w pewnym momencie zawsze otrzymamy 1 lub 4. Zdefiniuj funkcję suma_kwadratow(int n), której wynikiem będzie suma kwadratów cyfr liczby podanej jako parametr. Przetestuj działanie dla liczby 123 i kilku innych liczb początkowych.