Treści usunięte z lekcji zgodnie z podstawą programową
z 2024 r. sprawdź w e-booku podręcznika na eduranga.pl.
z 2024 r. sprawdź w e-booku podręcznika na eduranga.pl.



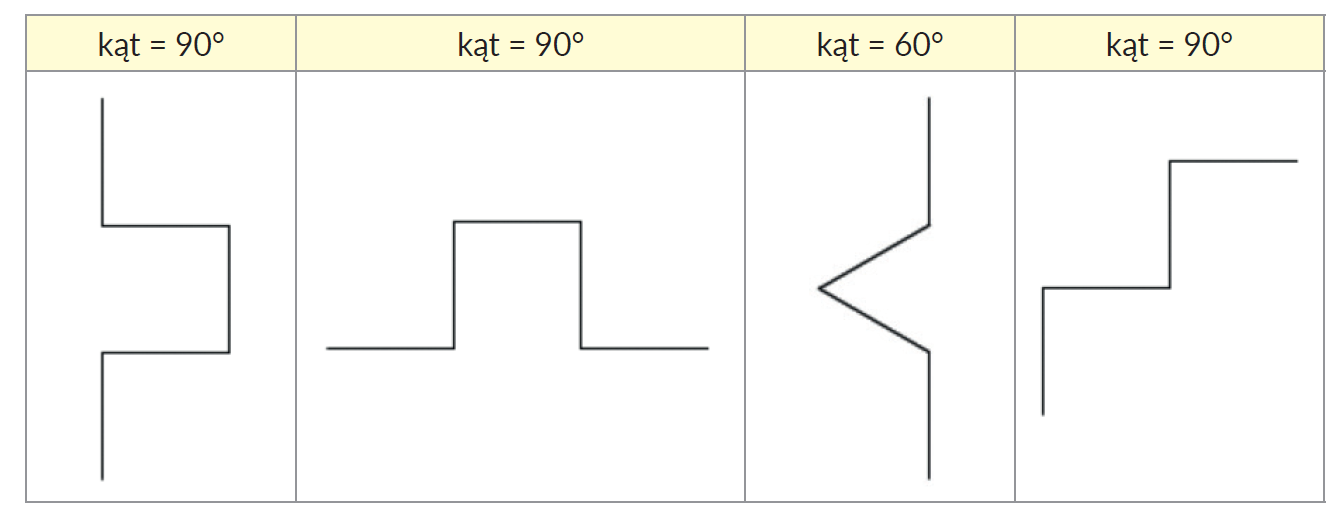
 Rysowanie polega na podawaniu kolejnych poleceń. Pierwsza kreska jest pionowa. W przypadku kwadratu (bok = d, kąt = 90°) ruchy żółwia można zapisać następująco: F+F+F+F. Zapis pozwalający narysować trójkąt równoboczny (bok = d, kąt = 60°) to: F++F++F.
Rysowanie polega na podawaniu kolejnych poleceń. Pierwsza kreska jest pionowa. W przypadku kwadratu (bok = d, kąt = 90°) ruchy żółwia można zapisać następująco: F+F+F+F. Zapis pozwalający narysować trójkąt równoboczny (bok = d, kąt = 60°) to: F++F++F.