InfografikaSystem dwudziestkowy Majów
Infografika przedstawia zasady zamiany liczb zapisanych w systemie dwudziestkowym Majów na liczby zapisane w systemie dziesiątkowym i odwrotnie.

Infografika przedstawia zasady zamiany liczb zapisanych w systemie dwudziestkowym Majów na liczby zapisane w systemie dziesiątkowym i odwrotnie.
Prezentacja przedstawia najważniejsze konstrukcje stosowane w języku Python.
Plansza zawiera podstawowe operatory działań i porównania oraz polecenia.
Film prezentuje sposób zapisywania liczb binarnych oraz algorytmy przeliczania liczb z systemu dwójkowego na dziesiątkowy i odwrotnie.
Film prezentuje implementację algorytmu zamiany liczby dwójkowej na liczbę dziesiątkową i odwrotnie.
W edytorze zakodowano w języku Python algorytm wypisywania od końca cyfr danej liczby. Porównaj ten algorytm z zamieszczonym poniżej algorytmem zamiany liczby zapisanej w systemie dziesiątkowym na liczbę zapisaną w systemie dwójkowym.
Zdefiniuj funkcję na10(dana), której parametrem jest liczba binarna w postaci napisu, a wynikiem – odpowiadająca jej liczba w systemie dziesiątkowym. Sprawdź działanie funkcji dla podanych poniżej parametrów.
na10("101010") jest 42.na10("110101") jest 53.Zdefiniuj funkcję na2(liczba), której parametrem jest liczba dziesiętna, a wynikiem – odpowiadająca jej liczba zapisana jako napis w systemie dwójkowym. Sprawdź działanie funkcji dla podanych poniżej parametrów.
na2(42) jest "101010".na2(53) jest "110101".Zdefiniuj funkcję na10(dana), której parametrem jest liczba zapisana w systemie ósemkowym, a wynikiem – odpowiadająca jej liczba zapisana w systemie dziesiątkowym. Sprawdź działanie funkcji dla podanych poniżej parametrów.
na10("174") jest 124.na10("362374") jest 124156.Zdefiniuj funkcję na8(liczba), której parametrem jest liczba dziesiętna, a wynikiem – odpowiadająca jej liczba zapisana w systemie ósemkowym. Sprawdź działanie funkcji dla podanych poniżej parametrów.
na8(124) jest "174".na8(124156) jest "362374".Obrazki można zapisać za pomocą zer i jedynek jako napis złożony ze słów, np. litera H to „010000010”. Negatyw obrazka to napis z zerami pozamienianymi na jedynki i jedynkami pozamienianymi na zera,
czyli „101111101”.
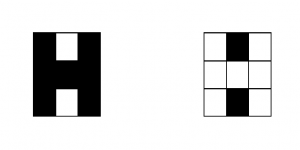
Napisz funkcję negatyw(kod), której wynikiem będzie kod negatywu danego obrazka. Sprawdź działanie funkcji dla podanych poniżej parametrów.
negatyw("010000010") jest "101111101".negatyw("101111101") jest "010000010".Napisz funkcję wieksza(liczba1, liczba2), której wynikiem jest większa z liczb podanych jako parametr lub dowolna z nich, gdy liczby są równe. Liczby są zapisane w systemie dwójkowym. Sprawdź działanie funkcji dla podanych poniżej parametrów.
wieksza("101","11") jest "101".wieksza("101","1111") jest "1111".Napisz funkcję bintooct(dana), której parametrem jest liczba zapisana w systemie dwójkowym, a wynikiem – odpowiadająca jej liczba zapisana w systemie ósemkowym. Postaraj się wykorzystać fakt, że 8 jest potęgą dwójki. Sprawdź działanie funkcji dla podanych poniżej parametrów.
bintooct("101010") jest "52".bintooct("110101") jest "65".Napisz funkcję octtobin(dana), której parametrem jest liczba zapisana w systemie ósemkowym, a wynikiem – odpowiadająca jej liczba zapisana w systemie dwójkowym. Postaraj się wykorzystać fakt, że 8 jest potęgą dwójki. Sprawdź działanie funkcji dla podanych poniżej parametrów.
octtobin("52") jest "101010".octtobin("65") jest "110101".