
Informatyka 3
Ćwiczenie 0
Przeanalizuj i popraw poniższy kod. Sprawdź działanie funkcji dla podanych poniżej parametrów.
- Wynikiem funkcji
ile(10)jest4. - Wynikiem funkcji
ile(100)jest7.
Ćwiczenie 1Pierwiastek kwadratowy
Zdefiniuj funkcję pierwiastek(x, eps), której parametrami są liczba dodatnia większa od liczby 1 lub jej równa oraz mała liczba dodatnia (np. 0,00001), a wynikiem jest ![]() z dokładnością
z dokładnością eps. Sprawdź działanie skryptu – wyznacz ![]() z dokładnością 0,1, 0,01 oraz 0,00001.
z dokładnością 0,1, 0,01 oraz 0,00001.
Ćwiczenie 2Dowolny pierwiastek
Zdefiniuj funkcję pierwiastek(x, n, eps), której parametrami są liczba dodatnia większa od liczby 1 lub jej równa, stopień pierwiastka oraz mała liczba dodatnia (np. 0,00001), a wynikiem jest ![]() z dokładnością
z dokładnością eps. Sprawdź działanie skryptu – wyznacz pierwiastek liczby 2 stopnia 2, 3 i 4 z dokładnością 0,1, 0,01 oraz 0,001.
Wskazówka: zmodyfikuj algorytm z ćwiczenia 1 – dodaj dodatkowy parametr n i podnieś c do n-tej potęgi.
Ćwiczenie 3Miejsce zerowe funkcji
Napisz program, za pomocą którego znajdziesz miejsce zerowe funkcji określonej wzorem f (x) = 2x3 – x – 5
w przedziale 〈0, 100〉 z dokładnością 0,001. Wykorzystaj algorytm połowienia.
Ćwiczenie 4Funkcja malejąca w przedziale
Napisz program, za pomocą którego znajdziesz miejsce zerowe funkcji określonej wzorem f(x) = – 1/4x2 + x + 2 w przedziale 〈2, 10〉 z dokładnością 0,001. Wykorzystaj algorytm połowienia. Wyznacz też miejsce zerowe przez obliczenie wyróżnika i porównaj oba wyniki. Możesz też poszukać drugiego miejsca zerowego w innym przedziale.
Ćwiczenie dodatkowe 1
Zmień kod z ćwiczenia 3 tak, aby badał miejsce zerowe podanej funkcji dla dowolnego zakresu <a, b>
z dowolną dokładnością eps. Sprawdź działanie funkcji dla różnych parametrów.
Ćwiczenie dodatkowe 2
Zmień kod z ćwiczenia 4 tak, aby badał miejsce zerowe podanej funkcji dla dowolnego zakresu <a, b>
z dowolną dokładnością eps. Sprawdź działanie funkcji dla różnych parametrów.
Zadanie 1Porównywanie ilorazów
Napisz funkcję porownaj(l1, m1, l2, m2), której wynikiem dla danych dwóch liczb l1/m1 oraz l2/m2 będzie 0 – gdy liczby są równe, 1 – gdy pierwsza liczba jest większa od drugiej, lub 2 – gdy druga liczba jest większa od pierwszej. Sprawdź działanie funkcji dla różnych parametrów.
Zadanie 2Szukanie pierwiastka
Napisz program, za pomocą którego znajdziesz ![]() z dokładnością eps i wyznaczysz liczbę kroków potrzebnych, aby otrzymać żądane przybliżenie. Sprawdź działanie funkcji dla
z dokładnością eps i wyznaczysz liczbę kroków potrzebnych, aby otrzymać żądane przybliżenie. Sprawdź działanie funkcji dla ![]() oraz dokładności 0,1, 0,01, 0,001 i 0,0001.
oraz dokładności 0,1, 0,01, 0,001 i 0,0001.
Zadanie 4Metoda Newtona-Raphsona
Innym algorytmem obliczania pierwiastka jest metoda Newtona-Raphsona. Znajdź informacje o tej metodzie i jej zastosowaniach, a następnie zaimplementuj ją do obliczania pierwiastka kwadratowego z liczby i sprawdź, czy jest wydajniejsza od metody połowienia.
Wskazówka
Znajdowanie pierwiastka kwadratowego można sprowadzić do szukania długości boku kwadratu o zadanym polu.

Szukany jest ![]() , czyli bok kwadratu o polu a. Jeżeli zacząć od prostokąta o bokach x i a/x, gdzie za x można przyjąć np. 1, to obliczanie kolejnych przybliżeń x pozwoli znaleźć szukany pierwiastek.
, czyli bok kwadratu o polu a. Jeżeli zacząć od prostokąta o bokach x i a/x, gdzie za x można przyjąć np. 1, to obliczanie kolejnych przybliżeń x pozwoli znaleźć szukany pierwiastek.
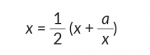
Dokładność można zweryfikować przez wyznaczenie różnicy długości boków prostokąta x – a/x.
Pytania quizoweMetoda połowienia
-
Do czego nie można zastosować metody połowienia?
-
-
W czym lepsza jest metoda połowienia w porównaniu z wyszukiwaniem liniowym?
-
-
Jak zachowuje się przedział poszukiwań na każdym etapie metody połowienia?
-